摘要: 平面扫描思想在计算几何,计算机图形学,网格计算等计算机理论领域有广泛的应用。有非常多的经典算法借助平面扫描的思想极大的降低了算法时间复杂度。例如线段相交问题、平面上多矩形轮廓算法、平面多矩形求交、空间冲突检测算法、Voronoi图构造算法、平面最近点对等等。
本文介绍了在ACM程序设计竞赛中经常用到的几个平面扫描算法。根据这些算法的作用,大致分为以下几类:
- 数据统计;
- 几何实体位置关系的检测;
- 最近点对。 本文依次选取了三类算法中具有代表性的经典算法加以介绍,并有针对性的剖析了大量经典ACM算法竞赛试题,以期对ACM程序设计竞赛参赛者起到抛砖引玉的作用。
关键字
平面扫描 ; ACM大学生程序设计竞赛 ; 算法 ; 数据统计 ; 几何实体位置关系; 最近点对
第一章:引言
ACM国际大学生程序设计竞赛(英文全称:ACM International Collegiate Programming Contest(ACM-ICPC或ICPC)是由美国计算机协会(ACM)主办的,一项旨在展示大学生创新能力、团队精神和在压力下编写程序、分析和解决问题能力的年度竞赛。经过近30多年的发展,ACM国际大学生程序设计竞赛已经发展成为最具影响力的大学生计算机竞赛。
竞赛的历史可以上溯到1970年,当时在美国德克萨斯A&M大学举办了首届比赛。当时的主办方是the Alpha Chapter of the UPE Computer Science Honor Society。作为一种全新的发现和培养计算机科学顶尖学生的方式,竞赛很快得到美国和加拿大各大学的积极响应。1977年,在ACM计算机科学会议期间举办了首次总决赛,并演变成为目前的一年一届的多国参与的国际性比赛。迄今已经举办了35届。
平面扫描思想是一种在计算几何、计算机图形学等领域经常用到的算法优化思想。由于ACM程序设计竞赛是一类对算法时间复杂度和空间复杂度要求非常高的高水平竞赛。竞赛中出现的许多的计算几何题目和高级数据结构题目都可以通过运用平面扫描的思想优化时空复杂度,使得程序能在题目给定的时间限制和空间限制下快速求出问题的解。
平面扫描算法一般由扫描线、事件点和当前扫描线事件点集合三个部分组成。扫描线一般是一根平行于坐标轴的水平线(或垂直线)。它按照从上到下(或从左到右)的顺序,依次检测事件点,通过删除或新增事件点来维护当前扫描线事件点集合。当前扫描线事件点集合通常都是用线段树、树状数组、红黑树等平衡二叉树来维护的,特殊情况下也需要用Hash表、块状表、跳跃链表等高级数据结构来达到维护目的。通过查询当前扫描线事件点集合的相关信息,我们就可以获得问题的答案。
正文将ACM竞赛中的扫描线算法分成三类,并依次介绍相关类型的算法。希望对参赛者的算法学习有所帮助。
第二章:算法介绍及试题剖析
第一节:数据统计
经典问题A 平面坐标系上有N个矩形,这些矩形的四条边都平行于X轴或Y轴。每个矩形可以被其他矩形部分或者完全遮盖,所有矩形合并成区域的边界周长称为轮廓周长。例如图1中所有矩形的轮廓如图2所示:
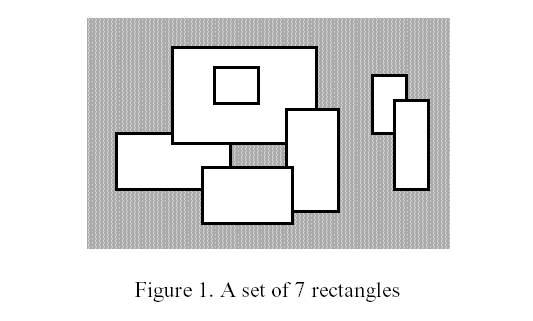
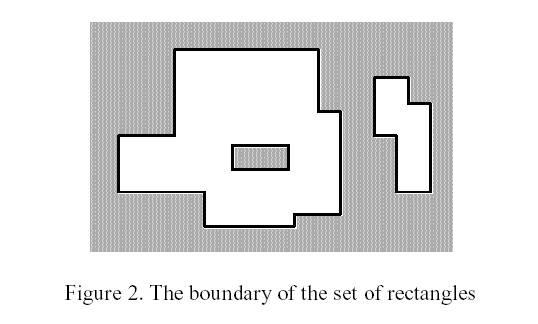
请设计一个算法,计算所有矩形的轮廓周长。
输入 平面上N个矩形,第i个矩形用左下顶点坐标(Xi, Yi)和右上顶点坐标(UXi, UYi)表示。
输出 所有矩形轮廓周长。
算法分析 先离散化。用每个矩形的四边所在直线将二维平面切割。这样,就只要考虑AB这样的单元线段了。把组成轮廓的单元线段长度相加就是矩形轮廓周长和。假设L1, L2 …, L8 各竖直线经过映射后对应于mapx1,mapx2 …, mapx8。为方便描述,令mapx0=mapx1。
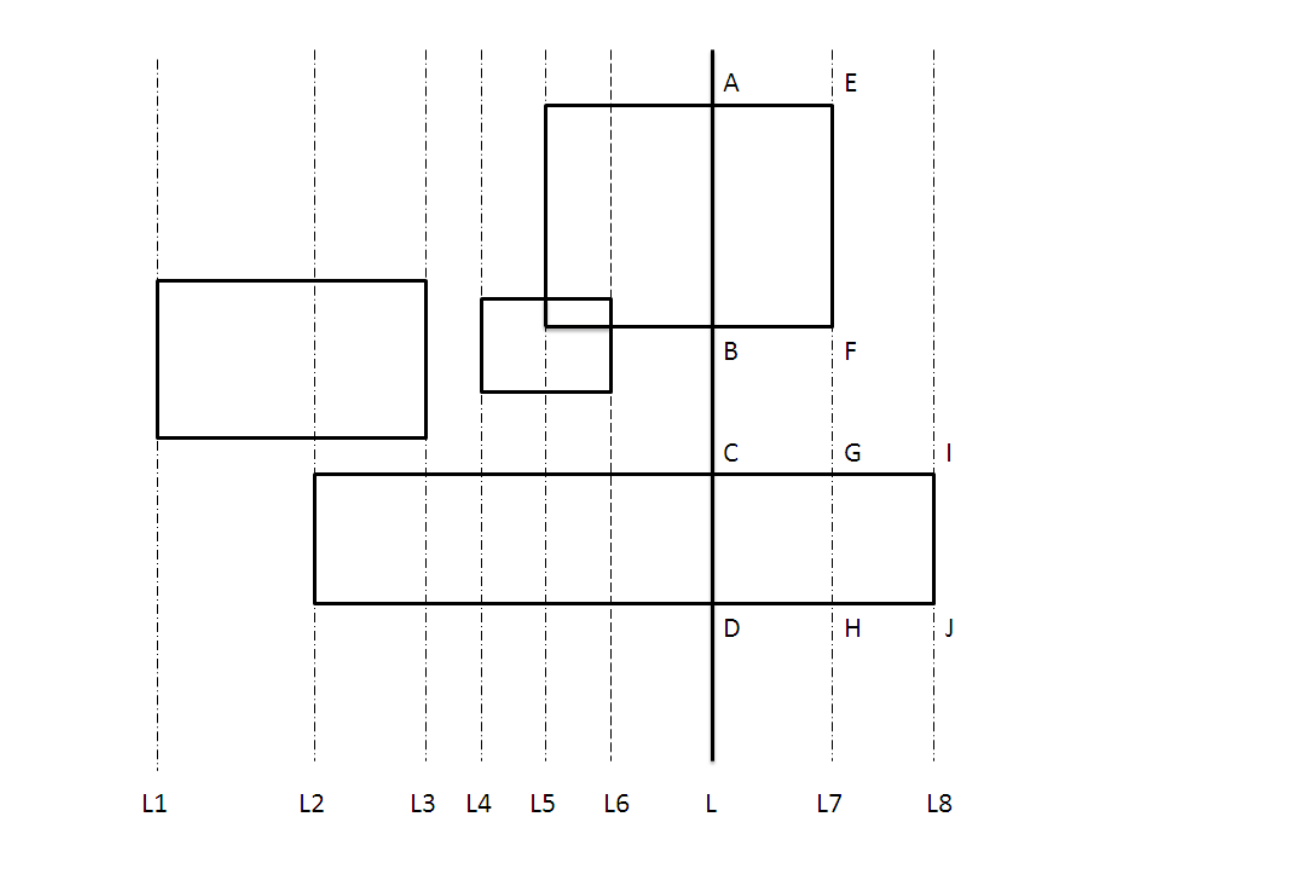
这样,考虑mapx(i-1)到mapxi之间的横向单元线段属于轮廓的总长度。在[mapx(i-1), mapx(i)]之间任作一竖直线L,将所有与L相交的矩形在L上的投影线段求并后的独立不相交线段数计为count,则共有2count(mapxi - mapx(i-1))长度的横向线段为轮廓长度。
例如,在L6和L7之间的作一条竖直线段L,与L相交的矩形有两个,它们在L上的投影分别为AB和CD,将AB和CD求并后,算出的独立不相交的线段数count=2。所以,在之间的横线单元线段属于轮廓的总长度就等于2count(L7-L6)=4*(L7-L6)。
通过上面分析,我们已经能够计算出所有轮廓周长中平行于x轴的总长度了。当然,可以通过类似的方法求出轮廓周长中平行于y轴的总长度。但是,在竖直线从左到右扫描的过程中,我们可以通过更为简洁的方法得到轮廓周长中平行于y轴的总长度。
考虑与L7相交的矩形在L7上的投影为[E,F]U[G,H],与L8相交的矩形在上的投影为[I,J],当竖直线扫描线从L7扫描到L8时,[E,F]就“露”了出来,成为竖直轮廓的一部分。这个[E,F]正好是L7上投影和L8上投影绝对值之差。如果相邻的扫描线的矩形投影分别为M1, M2 , 那么,在扫描过程中“露出”的纵向边长度为|M1-M2|。
综上所述,所有属于轮廓周长的横向边总长度和纵向边总长度已经可以计算出来,这样横向总长度和纵向总长度相加就是轮廓周长的总长度。
我们可以用扫描线从左到右依次扫描并更改相应状态的方式来描述这个计算过程。这里扫描线就是穿过各矩形竖直边的直线。事件点就是各矩形的竖直边,其中我们定义一个矩形的左边为插入事件,右边为删除事件。由于这里事件处理包括线段的插入和删除,所以当前扫描线事件点集合可以用一颗线段树来维护。 这颗线段树SegmentTree应该能够提供以下几种操作:
//初始化线段数stree
1. void Initialization(SegmentTree stree);
//往线段树stree插入[left,right]这条线段
2. void Insert(SegmentTree stree , int left , int right) ;
//删除线段树stree中[left,right]这一区间,该区间在删除前必须是被插入过的区间
3. void Delete(SegmentTree stree, int left, int right);
//询问线段树stree中所有存在区间求并后的独立不相交的线段数count。
4. int QueryCount(SegmentTree stree);
//询问线段数stree中所有存在区间求并后的总长度。
5. int QueryTotalLength(SegmentTree stree);
下面给出扫描线求矩形周长并的算法流程[代码参见附录A](至于线段树是如何进行上述五种操作的,请参考论文[1],这里不再赘述):
0. void rectangular_perimeter()
1. 以矩形定点坐标切割平面,实现横纵坐标的离散化并建立映射 mapx[0..2*N] , mapy[0..2*N] ;
2. 将所有事件点按照x坐标从左至右的顺序排好序。
3. Initialization( stree ) ; //初始化线段树
4. nowTotalLength = 0 ;
5. nowCount = 0 ;
6. Answer = 0 ;
7. for(i = 1 ; i <= 2*N ; ++ i){
8. if( Event[i] 是插入事件 )
9. Insert(stree , Event[i].down , Event[i].up ) ;//插入竖直线段[down,up]
10. else
11. Delete(stree , Event[i].down , Event[i].up ) ;//删除竖直线段[down,up]
12. nowTotalLength = QueryTotalLength( stree ) ;
13. nowCount = QueryCount( stree ) ;
14. Answer = Answer + lastCount * 2 * (mapx[i] - mapx[i-1]) ;
15. Answer = Answer + abs( nowTotalLength - lastTotalLength ) ;
16. lastTotalLength = nowTotalLength ;
17. lastCount = nowCount ;
18. }
20. return Answer ;
复杂度分析 假设矩形个数为N。第2行的排序复杂度为O(NlogN)。线段树提供四种操作:插入、删除、查询区间求并后的总长度、查询区间求并后的独立不相交线段数。这些操作的复杂度都为O(logN)。又总共有N个事件,所以总的复杂度为O(NlogN)。
矩形周长并问题是一个运用扫描线思想得到解决的经典例子。由矩形周长并算法衍生出来的ACM试题非常之多,其解答思路同样是通过扫描线从左到右扫描更新状态信息来获得问题的解。下面给出几个典型的应用。
例A.1
平面直角坐标系上有N个矩形,这些矩形的四边都平行于x坐标轴或者y坐标轴,每个矩形可以被其他矩形部分或者完全遮盖,求所有矩形合并成的区域的面积。(POJ1151)
算法分析
上题是求多矩形周长并,这题是就多矩形面积并。二者的解法上有着极大的类似。同样,先离散化:用每个矩形的四边所在直线将二维平面切割。将所有矩形的两条竖直边作为待扫描事件,其中左竖直边是插入事件,右竖直边是删除事件。 如图A.1所示,当扫描线为L时,将所有与L相交的矩形投影到L上,得到的投影线段为[A,B]U[C,D]。将该投影线段的长度之和记为length,则夹在竖直线L6和L7之间的面积为length * (L7-L6)。 在上题的线段树操作中,QueryTotalLength(stree)这个函数就可以把所有与扫描线相交的矩形在扫描线上投影的线段长度之和length求出来。 因此,可以将本题是上题的一个子问题。实现上只要稍作改变,就可以计算出多矩形面积并。[代码参见附录A.1]
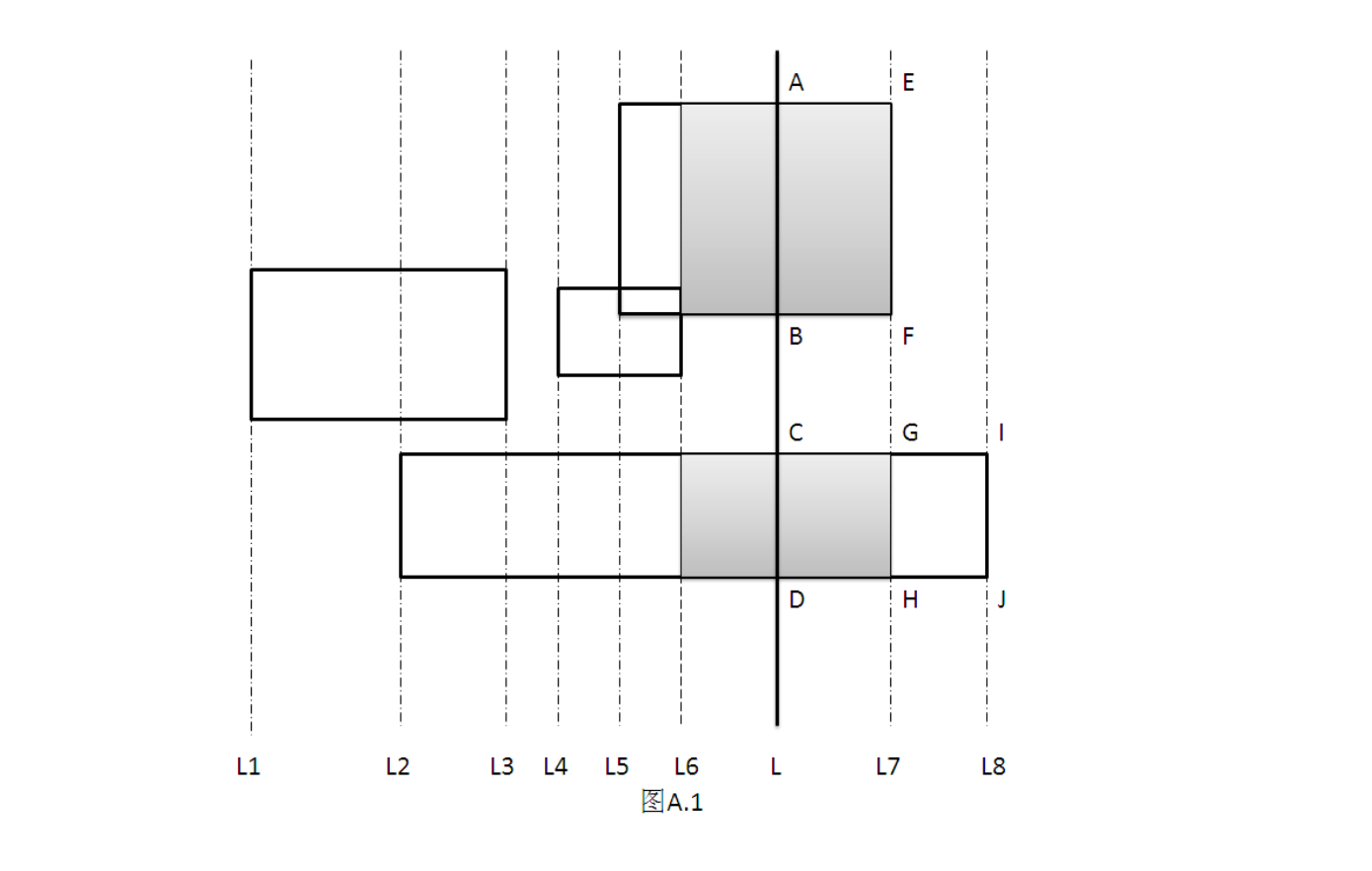
复杂度分析
复杂度同上,为O(NlogN)。
例A.2 你打算种些蔬菜到你的大农场上。但是,你自己太懒散,就雇佣了n个员工帮你种些种子。每个员工负责种一种种子到一块矩形土地上。不同员工做种植的区域可能重叠,所以重叠区域会被种植多种种子。但是,由于土地空间有限,同一区域的不同种子之间相互竞争,最后,只有最具竞争力的种子能生存下来。 现在有多种种子。不同的种子生长成为对应的蔬菜,每种蔬菜的价格互不相同。有一条这样的规律:越有竞争力的种子通常生长成价格越高的蔬菜。 你的任务是计算当你卖出你农场所有的蔬菜时,你有多少收入。(HDU 3255)
输入 n(1<=n<=30000),m(1<=m<=3)。其中n表示员工数,m表示种子种类。 然后一行有m个数,第i个数Price(i)表示第i种种子长成的蔬菜的价格(元/单位面积)。 接下来有n行,每行有X1,Y1,X2,Y2共5个数,表示一个员工的种植的矩形左下点为(X1,Y1),右上点为(X2,Y2),种的是第s种种子。
输出 计算出你的收入。
算法分析 这题可以这样思考:对第i个员工,他在矩形(X1,Y1,X2,Y2)内种植的是第s种种子。可以把该员工的种植情况想象成底面矩形(X1,Y1,X2,Y2)在XOY坐标系上且高为Price(s)的长方体。 这样,题目就转化成求N个底面在XOY坐标系上的长方体的体积并了。而计算体积时,可以用z=Price(i)平面依次去截N个长方体。求N个长方体被z=Price(i)平面截得的区域面积Area(i)就等价于多矩形面积并问题了(参考例A.1)。
于是,总体积就等于sigma{Area(i) * [Price(i) - Price(i-1)]}。其中Price(0)=0。
复杂度分析 最坏情况下,每次z=Price(i)都截到N个矩形。求矩形面积并的时间复杂度为O(NlogN)。共要截m次,所以总的时间复杂度为O(MNlogN)。[代码参见附录A.2]
例 A.3 (HDU 3621)平面直角坐标系中有N个矩形,每个矩形可以被其他矩形部分或者完全遮盖。求恰好被K个矩形覆盖的区域面积。
输入 第一行N(1<=N<=10000), K(1<=K<=N); 接下来N行,每行有X1,Y1,X2,Y2四个数,表示矩形的左下点为(X1,Y1),右上点为(X2,Y2)。
输出 恰好被K个矩形覆盖的区域面积。
算法分析 乍看本题,感觉跟例A.1非常基本差不多,只不过例A.1中求的是K=1的情况,这里是对给定K,求被K个矩形覆盖的面积。
的确,两个题目的扫描线,事件点都是一样的。但是,例A.1中的解法是建立在充分利用线段树能快速地插入线段、删除线段、查询多线段并的长度这一基础上的,而线段树并不能快速的查询被K条线段覆盖的区间长度。这使得我们不得不尝试着寻求其他的数据结构,这种数据结构能让我们快速地实现以下三大功能:插入线段、删除线段、查询被K条线段覆盖的区间长度。
事实上,块状链表是本题一个较好的选择。把整个Y轴分成长度约为sqrt(N)的小块,这样一条线段的中间部分会覆盖若干整个小块,两端的部分逐个元素处理。对每个小块,用一个hash表H维护被覆盖了i次的长度H(i),以及该小块作为整体被覆盖的次数q。查询时对每个小块查询H(k-q)即可。
复杂度分析 块状链表中,上述三种操作的时间复杂度都为sqrt(N)。所以,总的时间复杂度为O(N*sqrt(N))。 [代码参见附录A.3]
经典问题B 在平面直角坐标系中,有N个点(x,y)。每个点都带有一个权值weight。现在有一个高度为H,宽度为W且边都平行于x坐标轴或者y坐标轴的矩形。请问把矩形放在哪个位置,能够使得该矩形所覆盖住的点的权值和最大(这里点正好在矩形的边上不看做在矩形的内部)?
输入 第一行:N W H 三个整数分别表示点的个数,矩形的宽度,矩形的高度。接下来N行,每行有三个整数(x,y,weight)表示该点(x,y)的权值为weight。
输出 一个整数,表示该矩形能覆盖住的点的最大权值。
__算法分析__本题要求的是用一个给定高度和宽度的矩形去覆盖点,使得矩形内的点权和最大。于是,可以考虑用两条扫描线Left, Right来扫描坐标系中的点,同时,在扫描过程中确保两扫描线间距离不超过W-1。如图B1所示
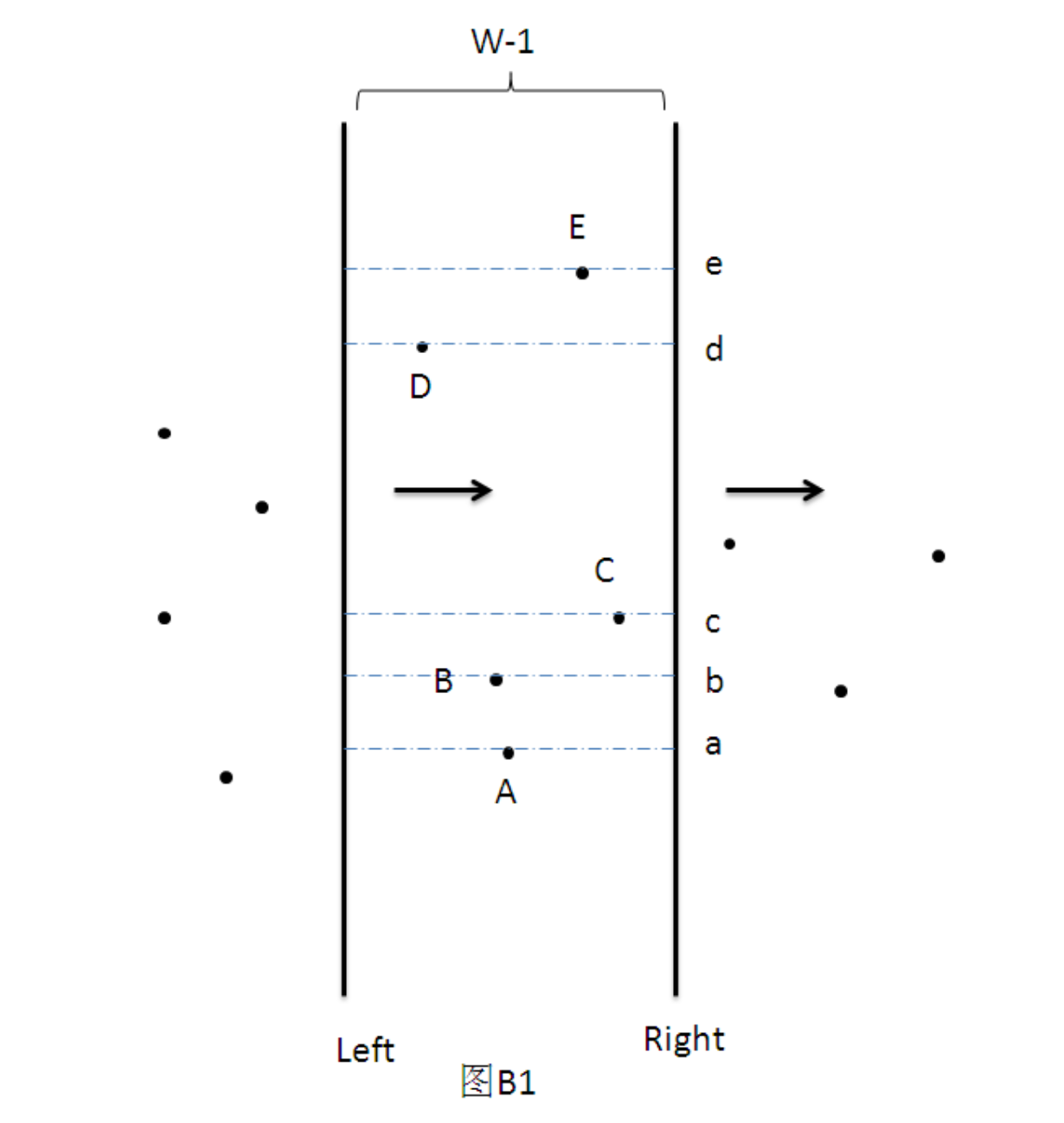
现在,我们来考虑x属于[Left,Right]区间的这些点组成的点集,在图B1中,点集S={A,B,C,D,E}。将S中的所有点都映射到Y轴上,得到一维点集MAPy(S)={a,b,c,d,e}。
现在问题转化成:在一维数轴上有K个点和一条长度为H的线段,问将线段放在什么位置能使得该线段覆盖住的点的权值和最大?
如图B2所示,在数轴上有点集S={a,b,c,d,e},它们对应的权值为W={3,2,5,6,3}。将S中的每个点x分成两个点x和x+H,其中若x的权值为w(x),则x+H的权值为-w(x), 于是: S1={a,a+H,b,b+H,c,c+H,d,d+H,e,e+H}, W1={3,-3,2,-2,5,-5,6,-6,3,-3}
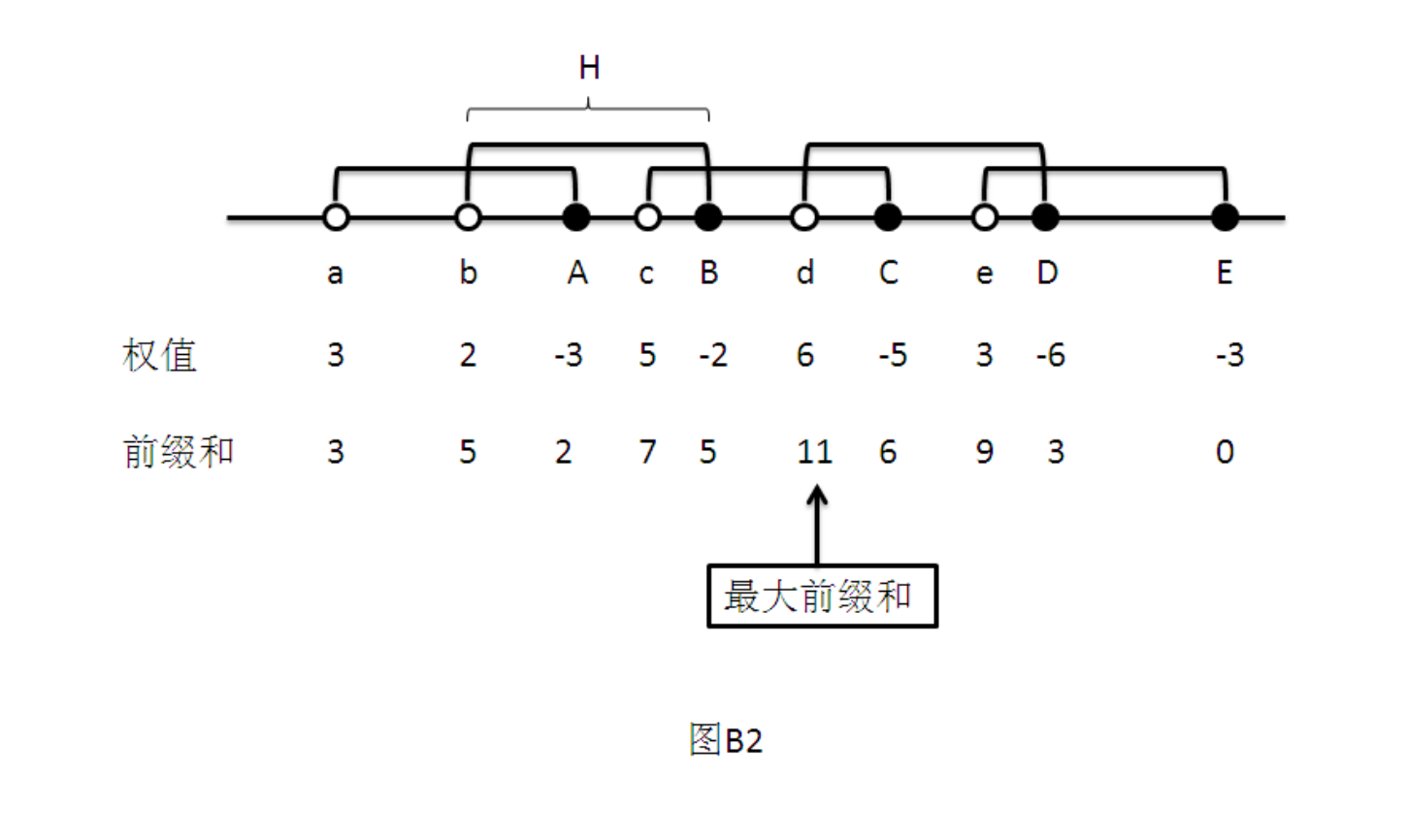
这样,将点的权值按照该点在数轴上的位置,从左至右排列好。求出该数列的最大前缀和,就是答案。理由很简单:把每个点x分成两个点x和x+H时,对应权值为w(x)和-w(x)。事实上,+w(x)表示该点进入长度为H的线段的覆盖区,-w(x)表示该点退出长度为H的线段的覆盖区。把长度为H的线段从左往右移动时,就相当于计算图中的前缀和。
综上所述,本题解法大致如下:用两根竖直扫描线Left,Right从左至右依次扫描各个坐标点,当然必须保证在任意时刻Left和Right之间的横向距离不超过W-1。然后用一颗线段树或者平衡二叉树来维护Left和Right之间的点,查询最大前缀和,取最大者就是答案。
在维护Left和Right之间的点时,要求的线段树或平衡二叉树tree必须支持如下操作:
void Init(); //初始化;
void Insert(int x ,int weight_x); //插入一维数轴上的点x的权值weight_x ;
void Delete(int x,int weight_x);//删除一维数轴上的点x的权值weight_x ;
int Max_Prefix() ;//查询当前数列中的最大前缀和;
tree实现上述操作1的时间复杂度为O(n);实现操作2,3的时间复杂度为O(logn);实现操作4的时间复杂度为O(1)。
算法流程描述如下:
0. int Max_Cover(Point p[] , int n , int W , int H)
1. 将 {p[0].y , p[0].y+H , ... , p[n-1].y , p[n-1].y + H }离散化到 my[] ;
2. 将 p[0..n-1]按照x从小到大的顺序排好序;
3. tree.init() ;
4. cur = ans = 0 ;
5. for(i = 0 ; i < n ; ++ i){
6. for(; cur < n ; ++ cur)
7. if(p[cur].x - p[i].x < W ){
8. tree.Insert( my[ p[cur].y ] , p[cur].w ) ;
9. tree.Delete( my[ p[cur].y+H ] , p[cur].w ) ;
10. ans = max(ans , tree.Max_Prefix() ) ;
11. }else break ;
12. tree.Insert(my[p[i].y] , p[i].w );
13. tree.Delete(my[p[i].y+H] , p[i].w ) ;
14. }
15. return ans ;
复杂度分析 第1行:离散化复杂度为O(NlogN)。 第2行:排序复杂度为O(NlogN)。 第6~11行:cur是只增不减的,每个坐标点只进出tree一次。该处复杂度不影响外层循环。 所以,总时间复杂度为O(NlogN)。[代码参见附录B]
第二节:几何实体位置关系的检测
经典问题 C 平面直角坐标系中有N个矩形。这些矩形的四边都跟x轴或者y轴平行,给出每个矩形在坐标系中的位置关系,请设计一个高效率的算法来判断在这N个矩形中是否存在两个矩形相交(这里矩形相交是指两个矩形至少有一个公共点,内嵌也属于相交)。
算法分析 这题用类似于例A.1的算法思路:用每个矩形的四边所在直线将二维平面切割。然后,将一条竖直线看作扫描线,将每个矩形的左边看作插入事件,将每个矩形的右边看作删除事件。由于题目目的是判断是否存在两个矩形有相交部分,所以每次遇到插入事件时,先判断一下该事件线段是否与前面的事件线段有公共部分,如果相交,则证明存在两个矩形相交,否则就把插入事件进行插入处理。对于删除事件,直接进行删除处理就行了。
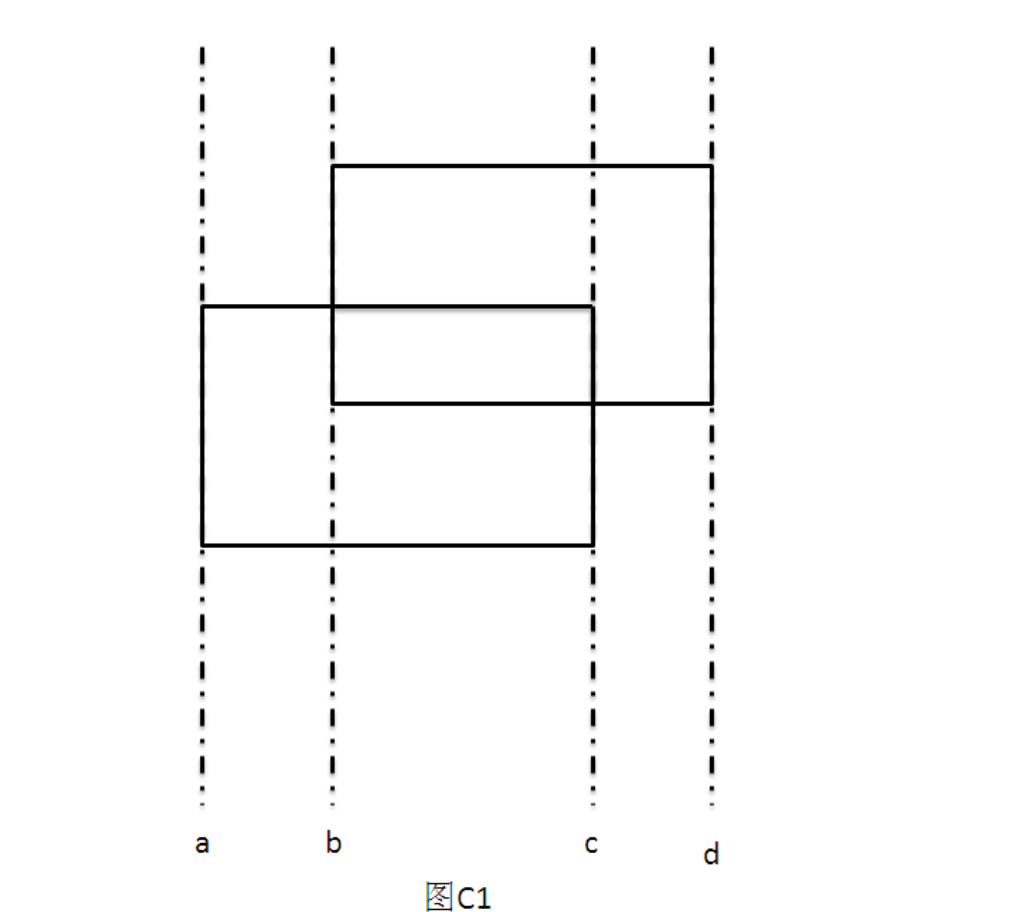
为了达到快速判断当前待插入事件线段是否与前面的事件线段相交这一目的,我们仍然可以选择用线段树来维护各插入线段。下面列出线段树应负责处理的操作,而不具体讨论线段树内部如何实现这些操作:
//初始化线段树;
void Init() ;
//插入线段[left,right];
void Insert(int left , int right);
//删除线段[left,right];
void Delete(int left , int right);
//判断当前存在的线段是否与[left,right]相交
void hasIntersect(int left , int right);
以下是算法流程描述:
00. boolean has_rectangle_intersect(rectangle r[] , int n)
01. 离散化{r[0].left_x , r[0].right_x , ... ,
r[n-1].left_x , r[n-1].right_x}到mapx[] ;
02. for( i = 0 ; i < n ; ++ i){
03. event[i<<1] = {r[i].left_x , r[i].down_y , r[i].up_y , +1 } ;
04. event[(i<<1)|1] = {r[i].right_x, r[i].down_y , r[i].up_y , -1 } ;
05. }
06. 将event[0..2*n-1]按照x从小到大的顺序排好序;
07. tree.init() ; //初始化线段树
08. for( i = 0 ; i < n<<1 ; ++ i){
09. if( event[i] 是插入事件 ){
10. if( tree.hasIntersection(event[i].down_y , event[i].up_y) )
11. return true ;
12. tree.Insert(event[i].down_y , event[i].up_y) ;
13. }else{
14. tree.Delete(event[i].down_y , event[i].up_y);
15. }
16. }
17. return false ;
复杂度分析
第1行:离散化复杂度为O(NlogN)。 第6行:事件排序复杂度为O(NlogN)。 第8~16行:对每个事件,进行插入删除复杂度为O(logN)。共有N个事件,所以该部分复杂度为O(NlogN)。 所以,总的复杂度为O(NlogN)。
经典问题 D 平面直角坐标系中有N个圆,任意两个圆之间只有内含和相离两种关系。给出每个圆的圆心坐标和半径,求出各圆之间的嵌套关系。 这里嵌套关系可以用一颗树来描述:当圆A内含于圆B的时候,则画一条从A指向B的有向线段,表示在关系树中A的双亲节点是B。例如下面图D1的关系树用图D2表示(R表示一个无穷大的圆,能够内含所有的N个圆)。
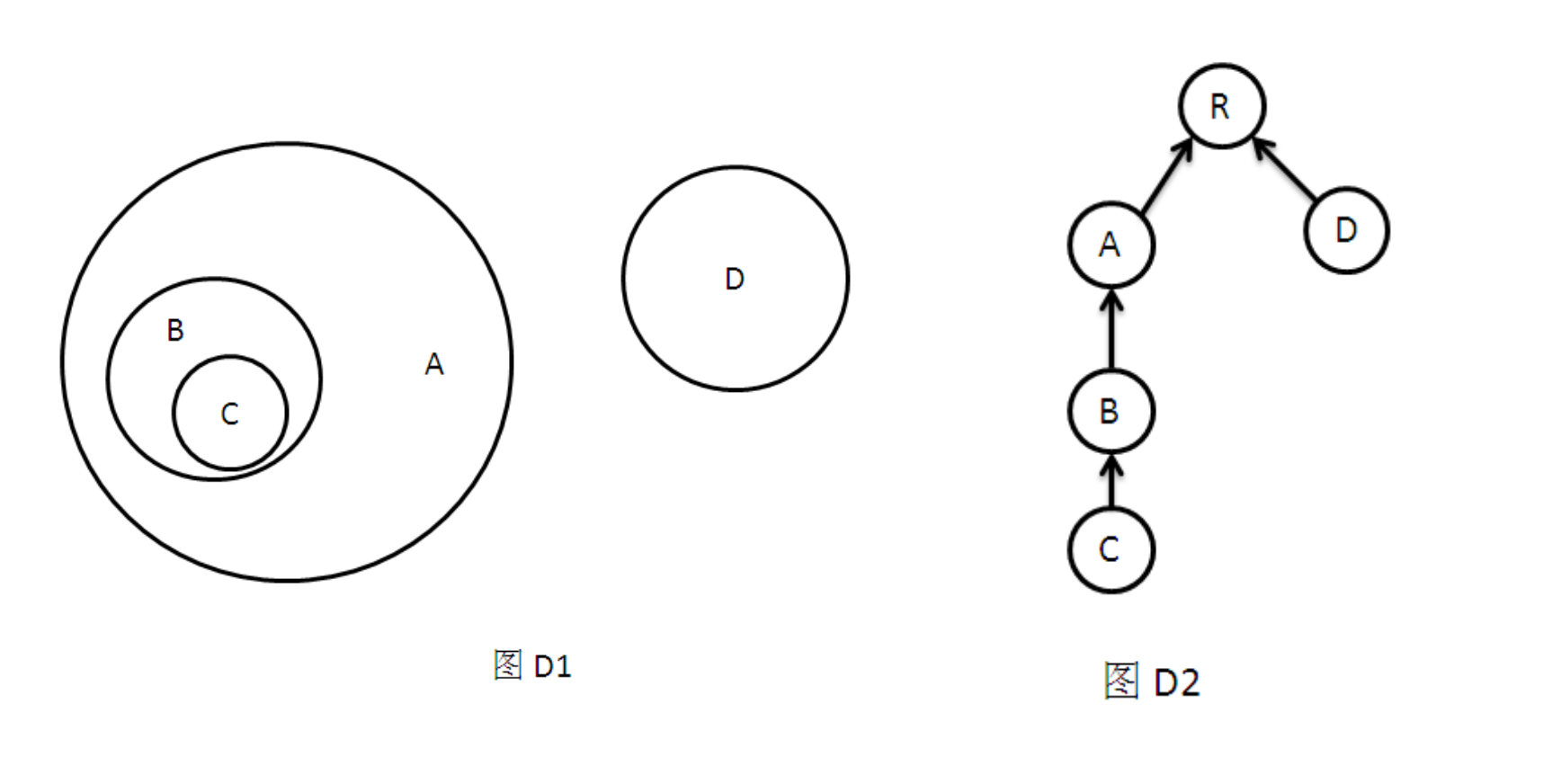
算法分析 想象一条垂直于x轴的扫描线从左到右扫描平面。对于每个圆(Xi,Yi,Ri),添加两个事件(Xi-Yi,Yi,-1)和(Xi+Yi,Yi,+1),分别表示该圆开始接触扫描线和离开扫描线的事件。对于某一时刻的扫描线,其余每个圆要么没有交点,要么有两个交点(相切的时候认为其为两个重合的交点)。用一个数据结构(平衡树)来保存当前扫描线与所有圆的交点位置,用+1和-1分别标记该交点为上交点还是下交点。按照x坐标从小到大的顺序处理每个事件,来模拟扫描线从左到右移动的过程。对于每个圆A接触扫描线的事件(Xi-Ri,Yi,-1),马上计算A的最小包含圆(父亲节点)。具体方法:在平衡树中查找一个与当前扫描线的交点小于Yi的最大值,若该交点为一个下交点,则该交点所属的圆B为圆A的最小包含圆,如图D3所示。否则该交点为一个上交点,则该交点所属的圆B为圆A的兄弟节点(在包含树上的关系),其父亲节点为圆A的最小包含圆,如图D4所示。
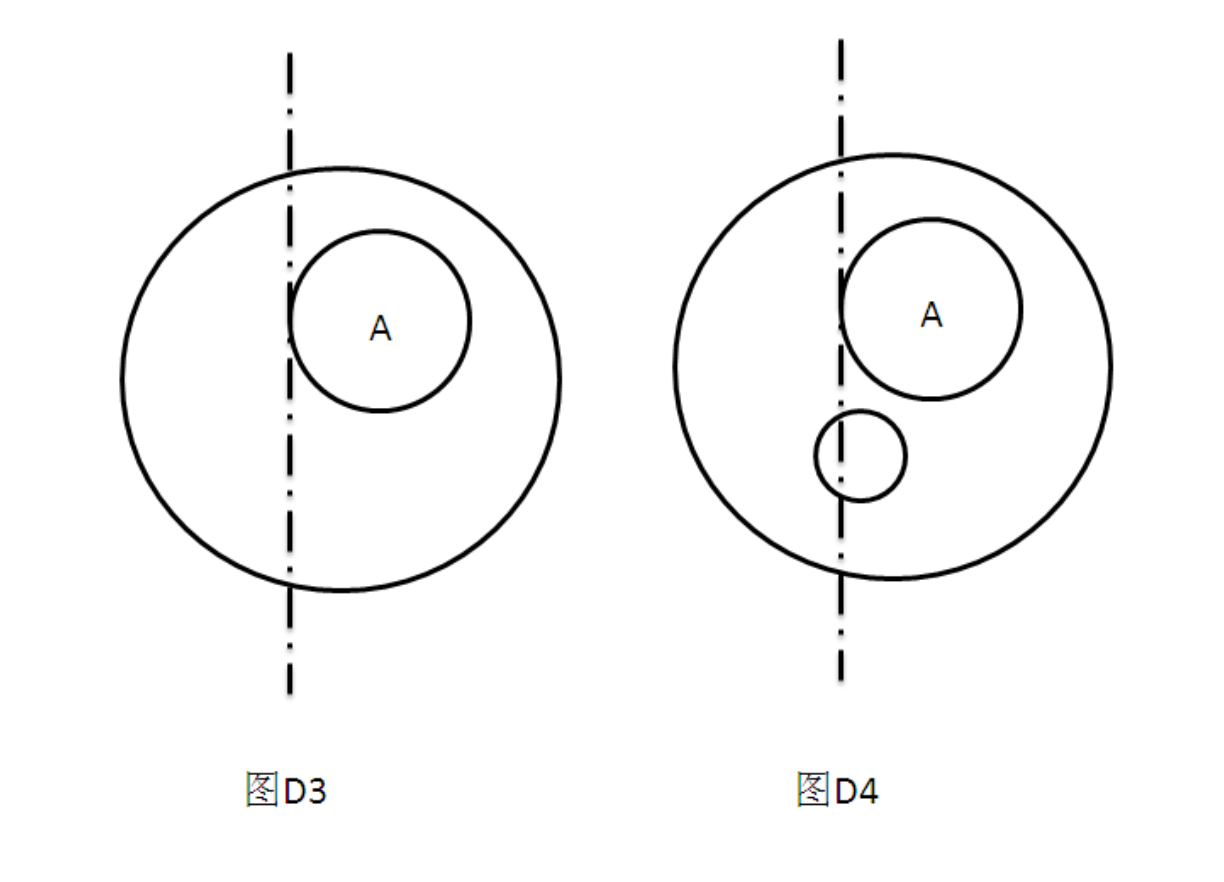
计算了圆A的最小包含圆后,将圆A与扫描线的两个交点插入到平衡二叉树中,表示扫描线在继续向右扫描的过程中与圆A有交点。对于圆A离开扫描线的事件,则简单地从平衡树中删除这两个交点即可。这样处理完所有事件后即可建立出需要的树结构(用父亲指针表示)。
算法流程分析:
00. int[] build_tree(circle c[] , int n)
01. for(i = 0 ; i < n ; ++ i){
02. event[2*i] = {i , c[i].x - c[i].r , c[i].y , -1 } ;
03. event[2*i+1] = {i , c[i].x - c[i].r , c[i].y , +1 } ;
04. }
05. 将event[0..2*n-1]按照x从小到大(x相等时,插入事件优先)的顺序排好序;
06. tree.init() ; //初始化树状结构
07. for(i = 0 ; i < 2*n ; ++i){
08. if(event[i]是删除事件){
09. tree.Delete( 该事件上交点 );
10. tree.Delete( 该事件下交点 );
11. }
12. if(event[i]是插入事件){
13. tree.Insert( 该事件上交点 );
14. tree.Insert( 该事件下交点 );
15. Down = tree.Below( 该事件下交点 ) ;
16. if( Down == NULL ){
17. father[ 当前事件所在圆 ] = 无穷大圆;
18. }else{
19. if( Down 是上交点 )
20. father[ 当前事件所在圆 ] = father[ Down所在圆 ] ;
21. if( Down 是下交点 )
22. father[ 当前事件所在圆 ] = Down坐在圆;
23. }
24. }
25. }
26. return father ;
复杂度分析
第5行:将2N个事件排序,复杂度为O(NlogN)。 第7~25行:对每个事件点进行插入删除处理,并通过平衡二叉树进行查询更新。复杂度为O(NlogN)。 所以,总的时间复杂度为O(NlogN)。[代码参见附录D]
第三节:最近点对
经典问题E 平面直角坐标系中有N个点,给出N个点的坐标,请设计一个高效算法计算最近点对距离。
算法分析 最近点对问题是计算几何中运用分治算法得到解决的经典问题。目前该问题已经证明的复杂度下界为O(NlogN)。对于分治算法而言,参考文献[2]中有详细的介绍。相比分治算法复杂繁琐的算法流程,用扫描线扫描思想得到的最近点对问题解决方案则要精炼简洁的多。但无论是分治算法还是扫描线算法,最近点对问题的解决都基于以下一条非常重要定理:
定理 设N个点p(1),p(2),…,p(n)按照x从小到大的顺序排好序。记p(1),p(2),…,p(i)的最近点对距离为d(i)。若现在已经计算出了d(i-1),则计算d(i-1)时,最多只需要计算6个p(i)左边的点与p(i)的距离,就可更新得到d(i)。
证明 显然d(i)<=d(i-1)。 若在p(1),p(2),…,p(i-1)中添加了p(i)后,能够得到更近的点对距离,那么必定是由于p(i)与p(1),p(2),…,p(i-1)中某个点之间距离比d(i-1)更小。 显然,p(1),p(2),…,p(i-1)中与p(i)距离比d(i-1)更小的点只可能位于S=[p(i).x-d(i-1),p(i).x] X [p(i).y-d(i-1), p(i).y + d(i-1)]这个区域内,下面证明该区域内的点不可能超过6个点。
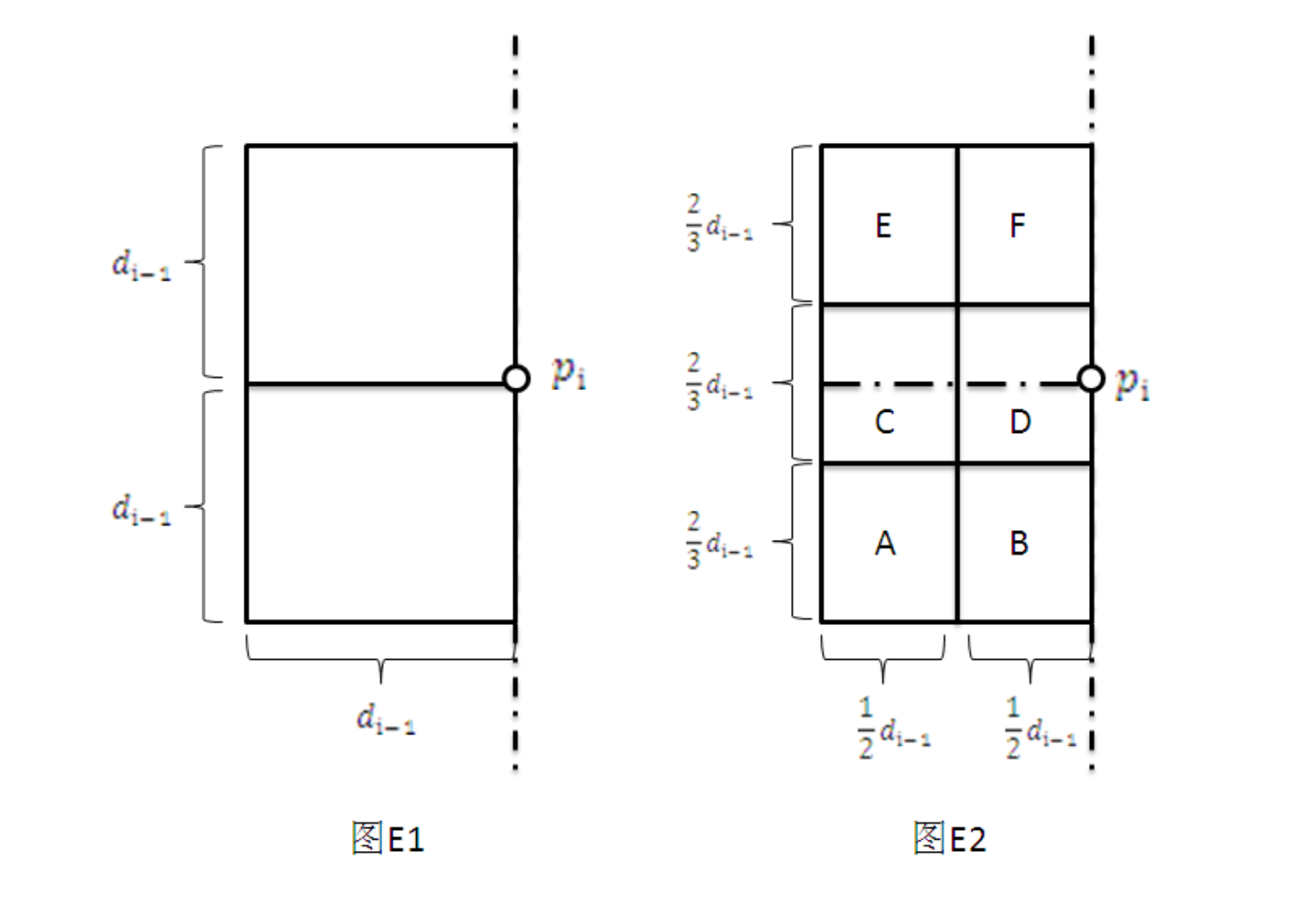
采用反证法。假设区域S内超过6个点,则将S区域划分成如图的6个区域,每个局域大小为:
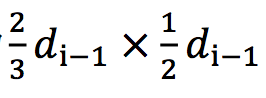
由抽屉原理知,必有2个点位于同一区域,设这两个点为p(j),p(k)。则
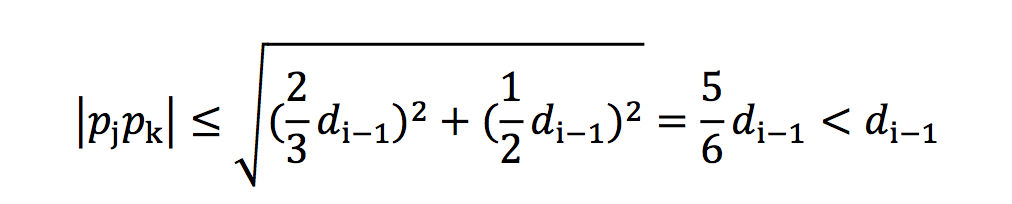
这样,就在p(1),p(2),…p(i-1)这些点中找到了p(j),p(k),而这两个点之间的距离比d(i-1)更小。这与d(i-1)定义矛盾。
综上,定理得证。
根据上述定理,每次更新d(i)得到更近的距离时,只要计算p(i)与常数(不超过6)个点的距离进行比较即可。问题是:如何才能找到p(i)“左附近”的这些点呢? 考虑一条从竖直扫描线从左到右依次扫描各个坐标点。用一颗平衡二叉树来维护当前事件点“左附近”的点。该平衡二叉树中的点按照y坐标较小优先的原则建树。这颗平衡二叉树BST提供如下操作:
Init();//初始化平衡二叉树
Insert(Point p); //插入一个点到BST中
Delete(Point p); //删除BST中点p
Lower_Bound(Point p);//找到不小于p的BST中的最小点
算法流程描述如下:
0. double closest_point(Point p[] , int n)
1. 将p[1],p[2]...p[n]这 n 个点按照x坐标从小到大排好序;
2. BST.Init() ; // 初始化平衡二叉树
3. BST.Insert( p[1] ) ; //将第一个点插入到 BST 中
4. left = 0 ;
5. distance = 无穷大 ; //初始化最近距离
6. for( i = 2 ; i <= n ; ++ i){
7. //控制BST中所有点与p[i]的水平距离不超过distance
8. while(left <= n && p[i].x - p[left].x >= distance )
10. BST.Delete( p[left] ) ;
11. q = BST.Lower_Bound( Point(p[i].x ,p[i].y-distance )) ;
12. while( q != BST.end() && q.y - p[i].y < distance ) {
13. //计算并更新新的distance .
14. distance = min(distance , dist( q , p[i])) ;
15. q = BST.next(q) ; //取得 q 的后继结点
16. }
17. }
18. return distance ;
复杂度分析
第三章:总结
平面扫描思想是算法设计中的一个非常重要的思想,它通过充分利用事物之间的相邻性,能够更清晰的展示问题的本质,因而能够达到优化算法的目地。
在论文正文中,作者从数据统计、几何实体位置关系的检测、最近点对三个应用层次,依次详细分析了5个经典问题,并剖析了与经典问题相对应的比赛试题。对每个经典问题,论文都有清晰细致的算法流程描述和详尽的时间复杂度分析,必要时给出了算法的证明。
正文中的扫描线算法基本由三个部分组成:扫描线、待扫描事件(一般有插入事件和删除事件)、维护当前扫描线相关事件(一般是平衡二叉树、线段树等树形结构,也有块状链表、跳跃表的情况)。事先将待扫描事件按照某个顺序排好序,然后扫描线依序扫描各事件。对不同类型的事件,将当前扫描线相关事件进行相应的维护。最后,通过查询当前扫描线相关事件的某些信息,就能计算得到问题的解的信息。扫描线算法正是在处理相邻事件的过程中,获知问题的答案信息的。
当然,扫描线算法的应用远不止正文中的几个经典问题。正如摘要所说,它在空间冲突检测算法、构造Voronoi图等计算几何问题上也有非常重要的应用。此外,扫描线算法在计算机图形学等领域也有广泛应用。
参考文献
[1] 《数据结构的选择与算法效率——从IOI98试题PICTURE谈起》作者: 陈宏 [2] 《算法设计与分析》 作者:王晓东 [3] 《国际大学生程序设计竞赛例题解(六)》 作者:郭嵩山、翁雨健、梁志荣、吴毅 [4] 《算法艺术与信息学竞赛》 作者:刘汝佳、黄亮 [5] 《计算几何:算法设计与分析》 作者:周培德 [6] 《应用数学译丛·计算几何:算法与应用》 作者:(荷)德贝尔赫(Berg,M.) 等 著 邓俊辉 译