本文从工程实现角度解析TokuDB的索引结构--分形树。 详细描述了ft-index的磁盘存储结构,ft-index如何实现Point-Query, Range-Query, Insert/Delete/Update操作, 并在描述过程中,试图从各个角度和InnoDB的B+树做详细对比。
分形树简介
分形树是一种写优化的磁盘索引数据结构。 在一般情况下, 分形树的写操作(Insert/Update/Delete)性能比较好,同时它还能保证读操作近似于B+树的读性能。据Percona公司测试结果显示, TokuDB分形树的写性能优于InnoDB的B+树), 读性能略低于B+树。 类似的索引结构还有LSM-Tree, 但是LSM-Tree的写性能远优于读性能。
工业界实现分形树最重要的产品就是Tokutek公司开发的ft-index(Fractal Tree Index)键值对存储引擎。这个项目自2007年开始研发,一直到2013年开源,代码目前托管在Github上。开源协议采用 GNU General Public License授权。 Tokutek公司为了充分发挥ft-index存储引擎的威力,基于K-V存储引擎之上,实现了MySQL存储引擎插件提供所有API接口,用来作为MySQL的存储引擎, 这个项目称之为TokuDB, 同时还实现了MongoDB存储引擎的API接口,这个项目称之为TokuMX。在2015年4月14日, Percona公司宣布收购Tokutek公司, ft-index/TokuDB/TokuMX这一系列产品被纳入Percona公司的麾下。自此, Percona公司宣称自己成为第一家同时提供MySQL和MongoDB软件及解决方案的技术厂商。
本文主要讨论的是TokuDB的ft-index。 ft-index相比B+树的几个重要特点有:
- 从理论复杂度和测试性能两个角度上看, ft-index的Insert/Delete/Update操作性能优于B+树。 但是读操作性能低于B+树。
- ft-index采用更大的索引页和数据页(ft-index默认为4M, InnoDB默认为16K), 这使得ft-index的数据页和索引页的压缩比更高。也就是说,在打开索引页和数据页压缩的情况下,插入等量的数据, ft-index占用的存储空间更少。
- ft-index支持在线修改DDL (Hot Schema Change)。 简单来讲,就是在做DDL操作的同时(例如添加索引),用户依然可以执行写入操作, 这个特点是ft-index树形结构天然支持的。 由于篇幅限制,本文并不对Hot Schema Change的实现做具体描述。
此外, ft-index还支持事务(ACID)以及事务的MVCC(Multiple Version Cocurrency Control 多版本并发控制), 支持崩溃恢复。
正因为上述特点, Percona公司宣称TokuDB一方面带给客户极大的性能提升, 另一方面还降低了客户的存储使用成本。
ft-index的磁盘存储结构
ft-index的索引结构图如下(在这里为了方便描述和理解,我对ft-index的二进制存储做了一定程度简化和抽象, 具体的二进制存储格式可以参考我的博客):
在下图中, 灰色区域表示ft-index分形树的一个页,绿色区域表示一个键值,两格绿色区域之间表示一个儿子指针。 BlockNum表示儿子指针指向的页的偏移量。Fanout表示分形树的扇出,也就是儿子指针的个数。 NodeSize表示一个页占用的字节数。NonLeafNode表示当前页是一个非叶子节点,LeafNode表示当前页是一个叶子节点,叶子节点是最底层的存放Key-value键值对的节点, 非叶子节点不存放value。 Heigth表示树的高度, 根节点的高度为3, 根节点下一层节点的高度为2, 最底层叶子节点的高度为1。Depth表示树的深度,根节点的深度为0, 根节点的下一层节点深度为1。
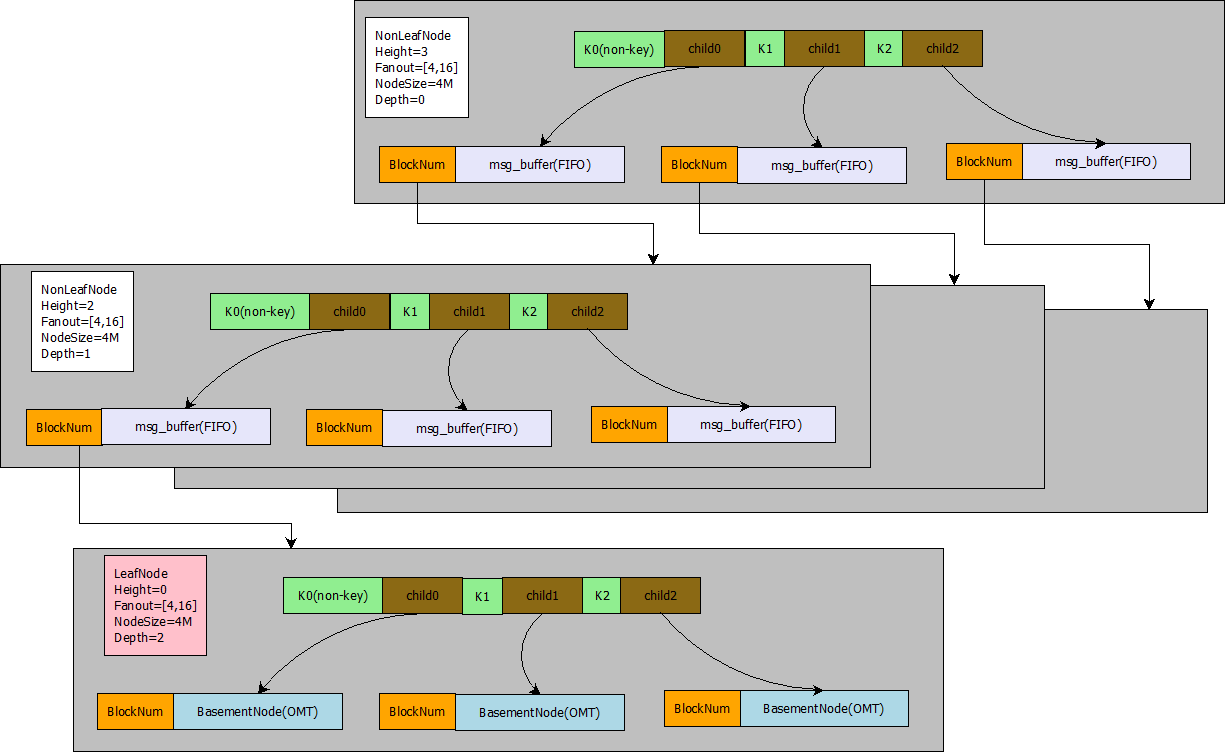
分形树的树形结构非常类似于B+树, 它的树形结构由若干个节点组成(我们称之为Node或者Block,在InnoDB中,我们称之为Page或者页)。 每个节点由一组有序的键值组成。假设一个节点的键值序列为[3, 8], 那么这个键值将(-00, +00)整个区间划分为(-00, 3), [3, 8), [8, +00) 这样3个区间, 每一个区间就对应着一个儿子指针(Child指针)。 在B+树中, Child指针一般指向一个页, 而在分形树中,每一个Child指针除了需要指向一个Node的地址(BlockNum)之外,还会带有一个Message Buffer (msg_buffer), 这个Message Buffer 是一个先进先出(FIFO)的队列,用来存放Insert/Delete/Update/HotSchemaChange这样的更新操作。
按照ft-index源代码的实现, 对ft-index中分形树更为严谨的说法是这样的:
- 节点(block或者node, 在InnoDB中我们称之为Page或者页)是由一组有序的键值组成, 第一个键值设置为null键值, 表示负无穷大。
- 节点分为两种类型,一种是叶子节点, 一种是非叶子节点。 叶子节点的儿子指针指向的是BasementNode, 非叶子节点指向的是正常的Node 。 这里的BasementNode节点存放的是多个K-V键值对, 也就是说最后所有的查找操作都需要定位到BasementNode才能成功获取到数据(Value)。这一点也和B+树的LeafPage类似, 数据(Value)都是存放在叶子节点, 非叶子节点用来存放键值(Key)做索引。 当叶子节点加载到内存后,为了快速查找到BasementNode中的数据(Value), ft-index会把整个BasementNode中的key-value都转换为一棵弱平衡二叉树, 这棵平衡二叉树有一个很逗逼的名字,叫做替罪羊树, 这里不再展开。
- 每个节点的键值区间对应着一个儿子指针(Child Pointer)。 非叶子节点的儿子指针携带着一个MessageBuffer, MessageBuffer是一个FIFO队列。用来存放Insert/Delete/Update/HotSchemaChange这样的更新操作。儿子指针以及MessageBuffer都会序列化存放在Node的磁盘文件中。
- 每个非叶子节点(Non Leaf Node)儿子指针的个数必须在[fantout/4, fantout]这个区间之内。 这里fantout是分形树(B+树也有这个概念)的一个参数,这个参数主要用来维持树的高度。当一个非叶子节点的儿子指针个数小于fantout/4 , 那么我们认为这个节点的太空虚了,需要和其他节点合并为一个节点(Node Merge), 这样能减少整个树的高度。当一个非叶子节点的儿子指针个数超过fantout, 那么我们认为这个节点太饱满了, 需要将一个节点一拆为二(Node Split)。 通过这种约束控制,理论上就能将磁盘数据维持在一个正常的相对平衡的树形结构,这样可以控制插入和查询复杂度上限。
注意: 在ft-index实现中,控制树平衡的条件更加复杂, 例如除了考虑fantout之外,还要保证节点总字节数在[NodeSize/4, NodeSize]这个区间, NodeSize一般为4M ,当不在这个区间时, 需要做对应的合并(Merge)或者分裂(Split)操作。
分形树的Insert/Delete/Update实现
在前文中,我们说到分形树是一种写优化的数据结构, 它的写操作性能要优于B+树的写操作性能。 那么它究竟如何做到更优的写操作性能呢?
首先, 这里说的写操作性能,指的是随机写操作。 举个简单例子,假设我们在MySQL的InnoDB表中不断执行这个SQL语句: insert into sbtest set x = uuid(), 其中sbtest表中有一个唯一索引字段为x。 由于uuid()的随机性,将导致插入到sbtest表中的数据散落在各个不同的叶子节点(Leaf Node)中。 在B+树中, 大量的这种随机写操作将导致LRU-Cache中大量的热点数据页落在B+树的上层(如下图所示)。这样底层的叶子节点命中Cache的概率降低,从而造成大量的磁盘IO操作, 也就导致B+树的随机写性能瓶颈。但B+树的顺序写操作很快,因为顺序写操作充分利用了局部热点数据, 磁盘IO次数大大降低。
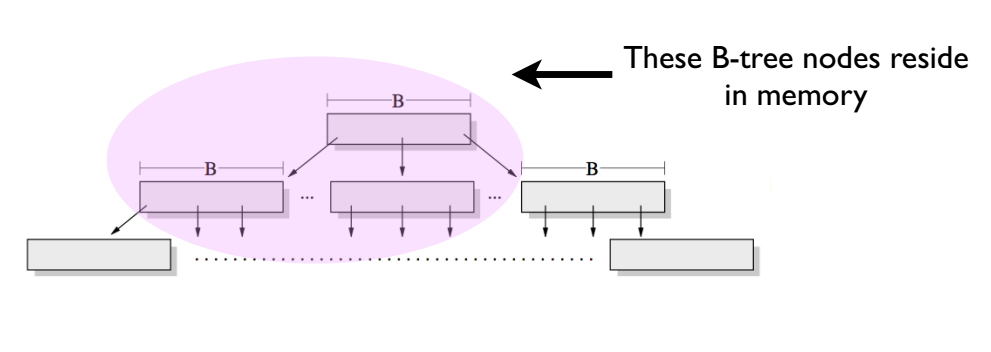
下面来说说分形树插入操作的流程。 为了方便后面描述,约定如下:
a. 我们以Insert操作为例, 假定插入的数据为(Key, Value);
b. 下文说的 加载节点(Load Page),都是先判断该节点是否命中LRU-Cache。仅当缓存不命中时, ft-index才会通过seed定位到偏移量读取数据页到内存;
c. 为体现核心流程, 我们暂时不考虑崩溃日志和事务处理。
详细流程如下:
- 加载Root节点;
- 判断Root节点是否需要分裂(或合并),如果满足分裂(或者合并)条件,则分裂(或者合并)Root节点。 具体分裂Root节点的流程,感兴趣的同学可以开开脑洞。
- 当Root节点height>0, 也就是Root是非叶子节点时, 通过二分搜索找到Key所在的键值区间Range,将(Key, Value)包装成一条消息(Insert, Key, Value) , 放入到键值区间Range对应的Child指针的Message Buffer中。
- 当Root节点height=0时,即Root是叶子节点时, 将消息(Insert, Key, Value) 应用(Apply)到BasementNode上, 也就是插入(Key, Value)到BasementNode中。
这里有一个非常诡异的地方,在大量的插入(包括随机和顺序插入)情况下, Root节点会经常性的被撑饱满,这将会导致Root节点做大量的分裂操作。然后,Root节点做了大量的分裂操作之后,产生大量的height=1的节点, 然后height=1的节点被撑爆满之后,又会产生大量height=2的节点, 最终树的高度越来越高。 这个诡异的之处就隐藏了分形树写操作性能比B+树高的秘诀: 每一次插入操作都落在Root节点就马上返回了, 每次写操作并不需要搜索树形结构最底层的BasementNode, 这样会导致大量的热点数据集中落在在Root节点的上层(此时的热点数据分布图类似于上图), 从而充分利用热点数据的局部性,大大减少了磁盘IO操作。
Update/Delete操作的情况和Insert操作的情况类似, 但是需要特别注意的地方在于,由于分形树随机读性能并不如InnoDB的B+树(后文会详细描述)。因此,Update/Delete操作需要细分为两种情况考虑,这两种情况测试性能可能差距巨大:
- 覆盖式的Update/Delete (overwrite)。 也就是当key存在时, 执行Update/Delete; 当key不存在时,不做任何操作,也不需要报错。
- 严格匹配的Update/Delete。 当key存在时, 执行update/delete ; 当key不存在时, 需要报错给上层应用方。 在这种情况下,我们需要先查询key是否存在于ft-index的basementnode中,于是Point-Query默默的拖了Update/Delete操作的性能后退。
此外,ft-index为了提升顺序写的性能,对顺序插入操作做了一些优化,例如顺序写加速, 这里不再展开。
分形树的Point-Query实现
在ft-index中, 类似select * from table where id = ? (其中id是索引)的查询操作称之为Point-Query; 类似select * from table where id >= ? and id <= ? (其中id是索引)的查询操作称之为Range-Query。 上文已经提到, Point-Query读操作性能并不如InnoDB的B+树, 这里详细描述Point-Query的相关流程。 (这里假设要查询的键值为Key)
- 加载Root节点,通过二分搜索确定Key落在Root节点的键值区间Range, 找到对应的Range的Child指针。
- 加载Child指针对应的的节点。 若该节点为非叶子节点,则继续沿着分形树一直往下查找,一直到叶子节点停止。 若当前节点为叶子节点,则停止查找。
查找到叶子节点后,我们并不能直接返回叶子节点中的BasementNode的Value给用户。 因为分形树的插入操作是通过消息(Message)的方式插入的, 此时需要把从Root节点到叶子节点这条路径上的所有消息依次apply到叶子节点的BasementNode。 待apply所有的消息完成之后,查找BasementNode中的key对应的value,就是用户需要查找的值。
分形树的查找流程基本和 InnoDB的B+树的查找流程类似, 区别在于分形树需要将从Root节点到叶子节点这条路径上的messge buffer都往下推(下推的具体流程请参考代码,这里不再展开),并将消息apply到BasementNode节点上。注意查找流程需要下推消息, 这可能会造成路径上的部分节点被撑饱满,但是ft-index在查询过程中并不会对叶子节点做分裂和合并操作, 因为ft-index的设计原则是: Insert/Update/Delete操作负责节点的Split和Merge, Select操作负责消息的延迟下推(Lazy Push)。 这样,分形树就将Insert/Delete/Update这类更新操作通过未来的Select操作应用到具体的数据节点,从而完成更新。
分形树的Range-Query实现
下面来介绍Range-Query的查询实现。简单来讲, 分形树的Range-Query基本等价于进行N次Point-Query操作,操作的代价也基本等价于N次Point-Query操作的代价。 由于分形树在非叶子节点的msg_buffer中存放着BasementNode的更新操作,因此我们在查找每一个Key的Value时,都需要从根节点查找到叶子节点, 然后将这条路径上的消息apply到basenmentNode的Value上。 这个流程可以用下图来表示。
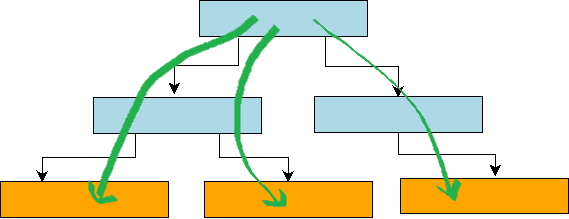
但是在B+树中, 由于底层的各个叶子节点都通过指针组织成一个双向链表, 结构如下图所示。 因此,我们只需要从跟节点到叶子节点定位到第一个满足条件的Key, 然后不断在叶子节点迭代next指针,即可获取到Range-Query的所有Key-Value键值。因此,对于B+树的Range-Query操作来说,除了第一次需要从root节点遍历到叶子节点做随机写操作,后继数据读取基本可以看做是顺序IO。
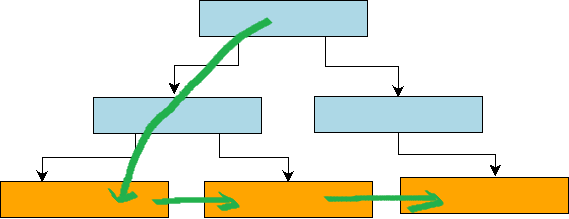
通过比较分形树和B+树的Range-Query实现可以发现, 分形树的Range-Query查询代价明显比B+树代价高,因为分型树需要遍历Root节点的覆盖Range的整颗子树,而B+树只需要一次Seed到Range的起始Key,后续迭代基本等价于顺序IO。
总结
本文以分形树的树形结构为切入点,详细介绍分形树的增删改查操作。总体来说,分形树是一种写优化的数据结构,它的核心思想是利用节点的MessageBuffer缓存更新操作,充分利用数据局部性原理, 将随机写转换为顺序写,这样极大的提高了随机写的效率。Tokutek研发团队的iiBench测试结果显示: TokuDB的insert操作(随机写)的性能比InnoDB快很多,而Select操作(随机读)的性能低于InnoDB的性能,但是差距较小,同时由于TokuDB采用有4M的大页存储,使得压缩比较高。这也是Percona公司宣称TokuDB更高性能,更低成本的原因。
另外,在线更新表结构(Hot Schema Change)实现也是基于MessageBuffer来实现的, 但和Insert/Delete/Update操作不同的是, 前者的消息下推方式是广播式下推(父节点的一条消息,应用到所有的儿子节点), 后者的消息下推方式单播式下推(父节点的一条消息,应用到对应键值区间的儿子节点), 由于实现类似于Insert操作,所以不再展开描述。
最后,欢迎对ft-index感兴趣的同学一起交流讨论。